The Application of Potential Energy for Creation of Power
Alexander V. Frolov
Professional physicist’s dislike for questions about applications of potential energy for power creation is understandable since they have a strong orientation to the Law of conservation of Energy.
This paper, without formulas demonstrates that there are no prohibitions to free energy in Nature. The availability of the potential field is a sufficient condition for creation of fuelless power systems. When such a system is in operation then certain effects show up that are connected with the Law of Conservation of Energy It is necessary now to formulate this Law in a general way. The problem of without-support (reactionless) motion may be solved by means of asymmetrical potential interaction which is also proposed.
1. The Total Work of a Potential Field
There are “incontestable” formulations: the work of potential field along closed trajectory is equal to zero. Indeed, from Figure 1 we can see that part of the work is positive (acceleration) and another part is negative (deceleration).
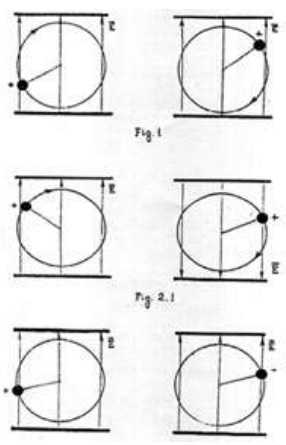
In physics textbooks the task of application of potential for making only positive work is not treated. This reluctance can be explained by unwillingness of textbooks authors to discuss more interesting question of energy transformations when the inner structure of space-time is changed.
Fig. 2 shows the same charged mass M rotating in potential electric field. The difference is in mode of interaction. The polarity of the interaction is changed when positive work is changed to negative.
Figure 2.1 shows that the direction of the field is changed and Fig. 2.2 shows that the sign of the charge is changed. There are simple examples of the application of potential field for creation of only positive work in a load. Fig. 3 depicts a scheme that is similar to water mill wheel.
Now let’s return to Fig. 1. Have you heard of the miller who submerged the mill wheel in the water flow of the river and then “scientifically” proved that it is impossible to use wafer flow for creation of power? Unfortunately, our school teachers use similar arguments!
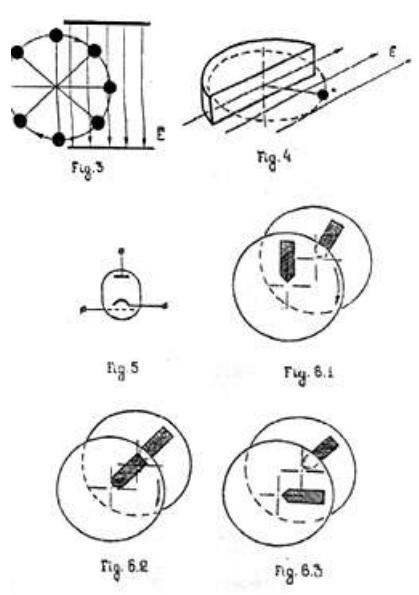
So, part of the trajectory or part of the periodical cycle that is part of negative work (deceleration) can be excluded by means of spatial superposition, pulsed mode operation, change of polarity of interaction, or by means of suitable screening (see Fig. 4). Fig. 5 shows that some changes in arrangement of electrodes in a vacuum tube allows one to increase energy of emission of the flow of electrons.
These schemes require certain development for industry application, of course. Note that Coulomb’s interaction is inversely proportional to square of distance so it is necessary to try to decrease this distance. Fig. 6 shows a version of a free energy device similar to a well-known electric machine. Let’s consider the interaction of two segments which have opposite charges, for example. In case of constant sign of interaction the process corresponds to the conclusions of the above miller (who immersed his mill wheel). Fig. 6.1 shows that attraction between segments create propulsion force and rotor moves with some acceleration, then Fig. 6.2 is at the point of balance and Fig. 6.3 shows that the rotor is decelerated since segments remain in attraction.
The total work of potential field is equal to zero. But why? It is not an indispensable condition of Nature. It is enough to change the sign of interaction between segments after balance point from attraction to repulsion to create the mode of acceleration again!
Let’s omit technological details and description of contacts, collector brushes, condenser, transformers and so on.
Above we considered examples of scalar electric potential application. If is possible to use any potential for it, for example vector potential of magnetic field and also the gravitational potential.
It is not new that a potential field can create work. Any textbook shows examples of negativepositive cycle of such work and proves that total work of successive acceleration and deceleration is equal to zero. But since it is successive performance of two processes it is conceptually possible to change parameters of one process to create cycle as sum of two or several parts of positive work. The solution lies in point-momentum of balance.
2. The Asymmetrical Potential Interaction.
Let’s consider the application of potential field for creation of propulsion force and withoutsupport (reactionless) motion. Fig. 7 is a scheme using ordinary flat electric condenser.
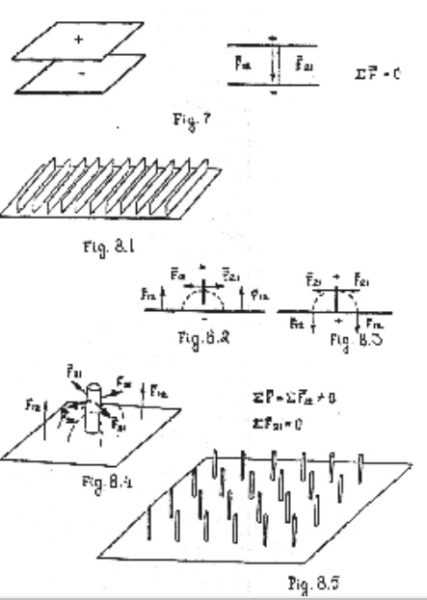
Two flat plates are in attraction (different charges) or in repulsion (same charges). Total force equals zero and the material system of the condenser remains stationary. All we need to find a solution is to note that the force line of potential field always is perpendicular to the charged surface. Fig. 8 shows the same condenser but one plate is perpendicularly turned to another plate.
The vertical plate is divided into several elements to decrease the distance of Coulomb’s interaction between plates. Total force that influence any vertical element is the sum of opposite forces and it is equal to zero. But total force that is applied to another (horizontal) plate is sum of co-directional elementary forces and it is not equal to zero. The system can be caused to move by means of asymmetrical potential interaction.
Note that perpendicular elements can have a cylindrical shape. The propulsion force can be regulated by means of changing the angle between plates of an asymmetrical condenser or by means of changing potential.
The well-known experiments with “inertioidal” moving systems can be considered as a particular case of asymmetrical (vector) potential technology. When eccentric mass is moving along epicycloidal or cardioidal heart-shaped trajectory, the trajectory creates a propulsion force that is the result of the gradient of acceleration. This process has been described by using a vector potential concept. Since asymmetrical scalar potential interactions do not require additional power after its creation, the scalar technology is more interesting for spacecraft applications than inertioidal systems.



